Если вы только начинаете изучать программирование, то можете столкнуться с "неочевидным" поведением ваших программ, особенно при работе с вещественными числами.
Самый популярный пример, иллюстрирующий эту проблему - сравнение 0.1 + 0.2 с 0.3. Для большинства людей очевидно, что 0.1 + 0.2 равно 0.3, поэтому ожидается, что это выражение вернет истину. Однако, если вы запустите его в Java, то результат может вас удивить:
System.out.println(0.1 + 0.2 == 0.3); // falseЭто выражение выводит false! Но почему? Если мы выведем на консоль результат выражения 0.1 + 0.2, то увидим следующее:
System.out.println(0.1 + 0.2); // 0.30000000000000004Вместо ожидаемых 0.3 мы получили 0.30000000000000004. Но не спешите отказываться от Java: эта проблема будет присутствовать во многих языках программирования. Дело не в языке программирования, а в том, как компьютер работает с данными и хранит их.


Как компьютер хранит данные
А почему так произошло? Для начала следует понять, как данные хранятся в памяти компьютера. Это происходит в формате двоичного кода.
Давайте в качестве примера возьмем число 6.25 и переведем его в двоичный код. Для этого нужно целую часть делить на 2, записывая остаток от деления, а дробную часть умножать на 2, после чего записываем целую часть, а дробную продолжаем умножать на 2.
Визуализация перевода 6.25 в двоичную систему счисления
Таким образом, 6.25 в двоичном виде становится 110.01. Однако здесь появляется проблема: в мире нулей и единиц не существует представления для десятичной запятой, поэтому компьютер не сможет сохранить такое число в памяти в том виде, в котором мы привыкли его видеть.
Стандарт IEEE-754
Для представления вещественных чисел в формате, который позволит преобразовывать их в простую последовательность нулей и единиц без всяких дополнительных знаков, ученые разработали систему чисел с плавающей запятой. Этот стандарт получил название IEEE-754 (wiki).
Согласно этому стандарту, двоичное число представляется в виде формулы:
(-1)s × M × BE,
где s — знак числа, M — мантисса, B — основание, E — экспонента. Поскольку мы работаем в двоичном коде, основание равно двум, и формула принимает следующий вид:
(-1)s × M × 2E.
Разбираемся на пальцах 🖐
Может показаться, что все эти формулы сложны, но на самом деле принцип довольно прост. Вещественное число мы должны сохранить как три отдельных числа: знак, экспоненту и мантиссу. Количество бит для хранения всегда ограничено форматом. Рассмотрим формат, в котором доступно 32 бита: 1 бит знака, 8 битов для экспоненты и 23 бита для мантиссы. Этот формат называется "одинарной точностью".

Чтобы привести наше число 110.01 к формуле, нам нужно сдвинуть запятую влево настолько, чтобы в целой части была единица. При этом каждый сдвиг увеличивает степень основания. Именно поэтому эти числа называются числами с плавающей запятой 🙃
Несмотря на то, что основание равно 10, это на самом деле представление 2 в двоичной системе счисления. Для удобства восприятия я не стал переводить степень этой двойки в двоичную систему счисления.
В итоге мы получаем 1.1001 x 22. Здесь 1.1001 - это наша мантисса, а поскольку наше число положительное, бит знака будет равен 0.
Уже в первых машинах использовались прием, который позволял не сохранять целую часть числа, так как она всегда равна единице. Такое представление называется "нормализованным". Оно позволяет экономить целый бит памяти, увеличивая точность представления числа. Кстати, основание всегда равно 10, поэтому его тоже не нужно сохранять.
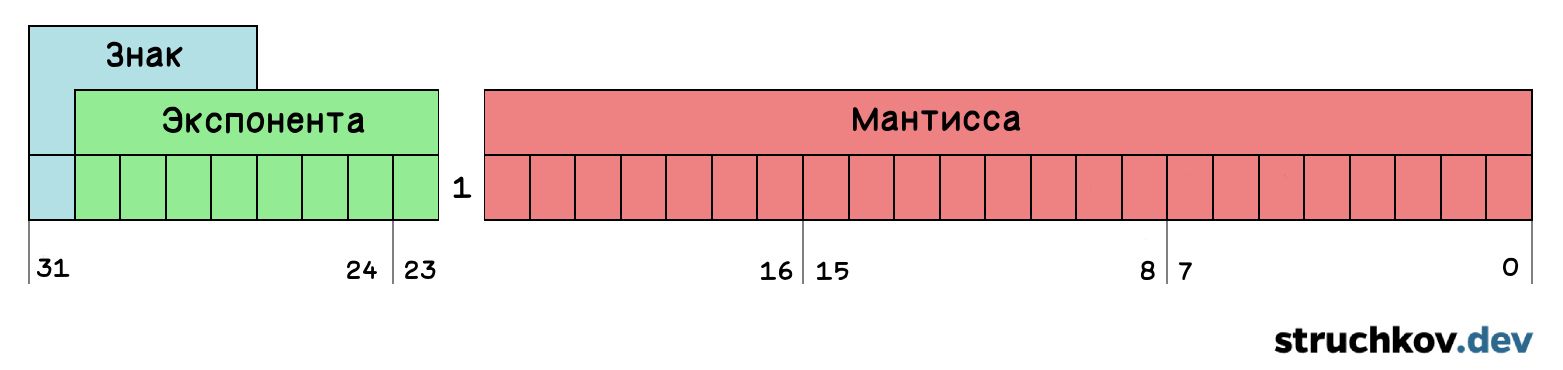
Таким образом, нормализованное число имеет следующий вид:
(-1)s × 1.M × 2E
Полученную дробную часть мы записываем в мантиссу, при этом целую часть мы не записываем, поскольку она всегда равна единице.
Чтобы получить экспоненту, к степени двойки прибавляют 127, и полученное число преобразуют в двоичный код.
Почему нужно прибавить 127?
Под экспоненту в нашем представлении чисел с плавающей запятой выделено 8 бит, что позволяет сохранить 256 различных значений. Экспонента может быть как положительной, так и отрицательной, и нам нужно сохранить ее знак. Однако в этом представлении не предусмотрено отдельного бита для знака экспоненты.
Возможно, вы знакомы с понятием дополнительного кода, который позволяет представлять отрицательные числа в двоичной системе. Однако, в данном контексте его использование затруднило бы быстрое сравнение чисел по старшему биту.
Решение этой проблемы состоит в хранении экспоненты относительно "середины" доступного диапазона значений. Для 8-битного диапазона этой "серединой" будет число 127. Если количество бит для экспоненты увеличится, "середина" будет соответствовать половине доступного диапазона значений.
Таким образом, все отрицательные степени будут располагаться левее числа 127, а все положительные - правее.

Итак, к нашей изначальной степени прибавляем 127 и получаем 129. Преобразуем 129 в двоичную систему счисления, и вот - мы получили экспоненту.
Также мы записываем бит знака. Напомню, что для положительных чисел этот бит равен 0, а для отрицательных - 1.
Таким образом, мы перевели вещественное число в двоичное представление. Казалось бы, нет никаких проблем. Однако, проблемы не возникли только потому, что в качестве примера было выбрано "удачное" число.
Неконвертируемые числа
Теперь попробуем преобразовать число 5.9 в двоичное представление. Это задача оказывается аналогичной попытке записать результат деления 1 на 3 в десятичной системе счисления. В обоих случаях мы столкнемся с периодической дробью: 5.9 в двоичной системе становится 101.11100(1100).
Однако, нам все равно нужно каким-то образом записать это число в память компьютера, которая, напомним, ограничена 32 битами. Это возможно сделать только путем отсечения той части числа, которая не помещается в 32 бита.
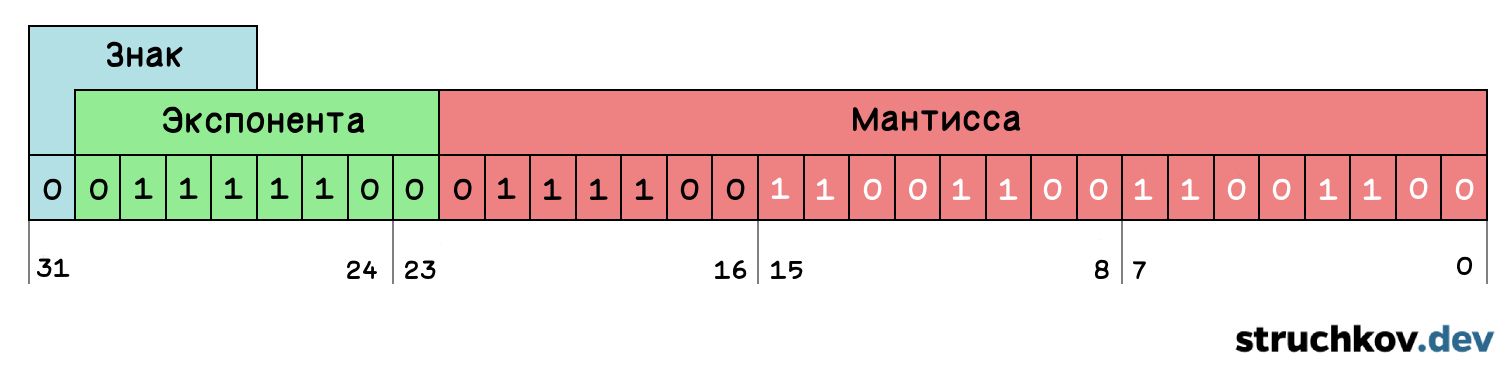
Попытаемся записать как можно больше повторений периода и затем восстановить из этой записи десятичное число.
5.89999961
Этот результат отличается от исходного числа 5.9. Такова особенность работы компьютеров: они могут оперировать вещественными числами только до определенной точности. И эта точность – единственное, чем мы можем манипулировать. Но как мы можем это сделать?
Ранее мы рассмотрели пример, когда у нас было 32 бита для записи числа, что соответствует одинарной точности (float в Java). Мы можем увеличить этот размер в два раза до 64 бит, что уже соответствует двойной точности (double в Java). Чем больше бит у нас будет для записи, тем более точное число мы сможем сохранить. Однако восстановить исходное число с абсолютной точностью все равно не удастся.
В математике между числами 1.0 и 2.0 существует бесконечное количество вещественных чисел. Однако, используя одинарную точность (float), компьютерная память способна точно сохранить лишь 8 388 609 чисел, находящихся между 1.0 и 2.0.
Неточности при вычислениях
Вернемся к нашему примеру с числами 0.1 и 0.2. Если попробуем преобразовать эти числа в двоичную систему счисления, то обнаружим, что они также не могут быть точно переведены. Используя специализированный точный калькулятор, можно получить максимально приближенные значения этих чисел в двоичной системе, представленные здесь в десятичной форме:
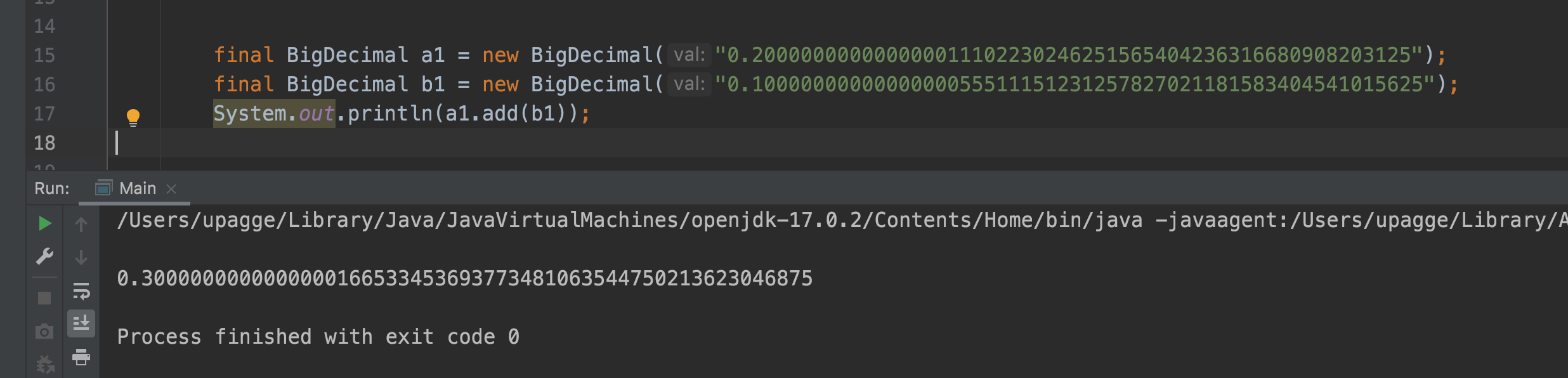
0.1 = 0.1000000000000000055511151231257827021181583404541015625
0.2 = 0.200000000000000011102230246251565404236316680908203125
Это максимально точные значения, которые может хранить компьютер. Если сложить эти числа, мы получим:
0.3000000000000000166533453693773481063544750213623046875
Это значение близко к нашему результату 0.30...04, но, если применить правила математического округления, мы должны были получить 0.30...02. Давайте посмотрим, что получится, если мы попытаемся вывести на консоль 0.30...02.
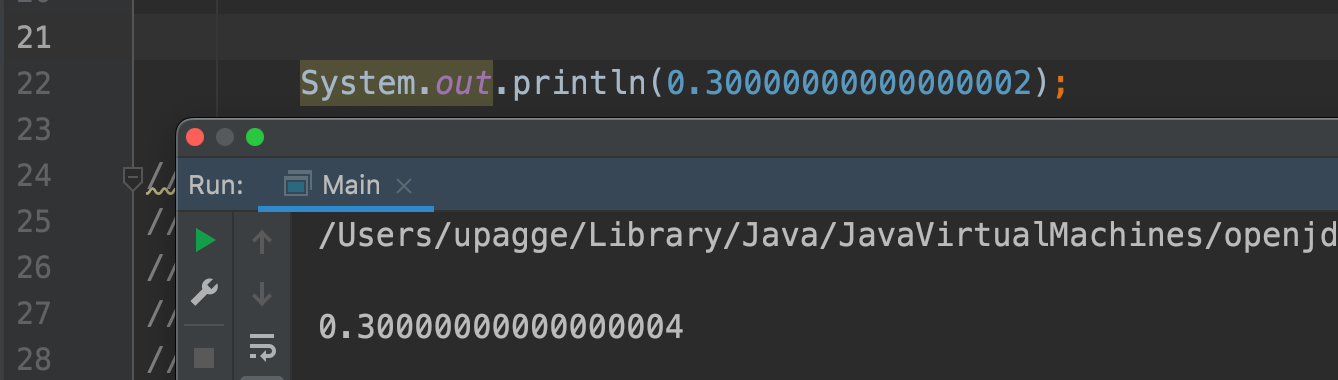
То число, которое мы получили в результате сложения, также не может быть точно сохранено. Ближайшее значение, которое может сохранить компьютер, равно
0.3000000000000000444089209850062616169452667236328125.
Отображение 0.1 при отладке
Вы могли заметить, что во время отладки значение переменной отображается как 0.1, а не 0.10...55.
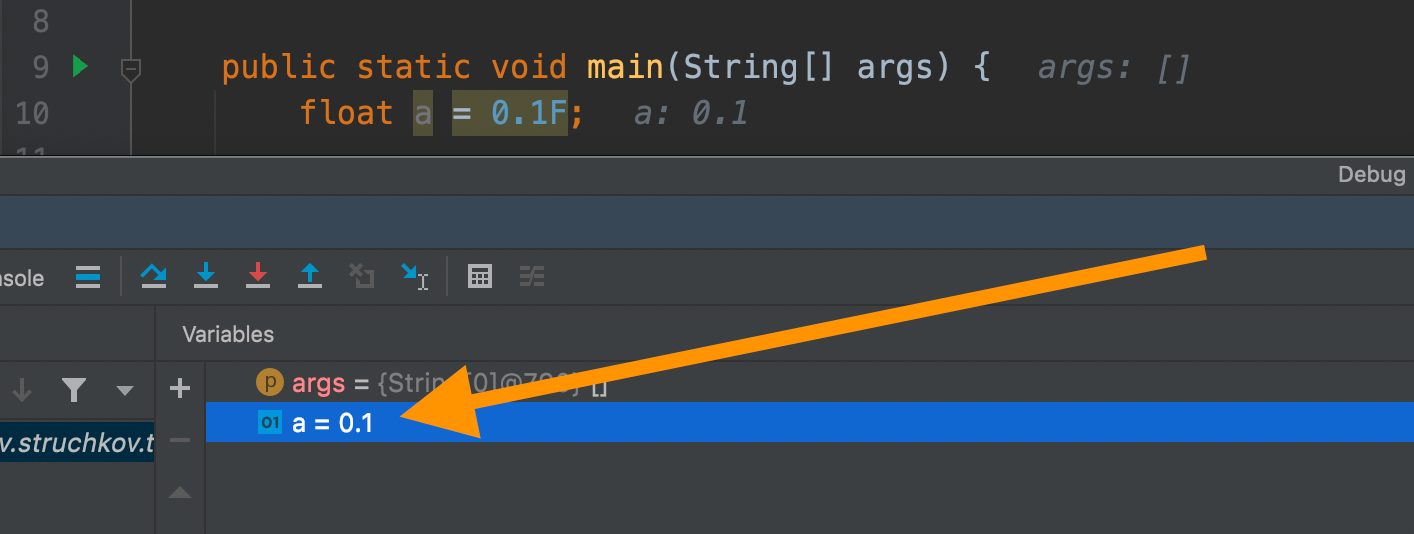
Однако это лишь способ визуализации данных. Если посмотреть, что на самом деле хранится в памяти этой переменной, то мы обнаружим обычную структуру с знаком, экспонентой и мантиссой.
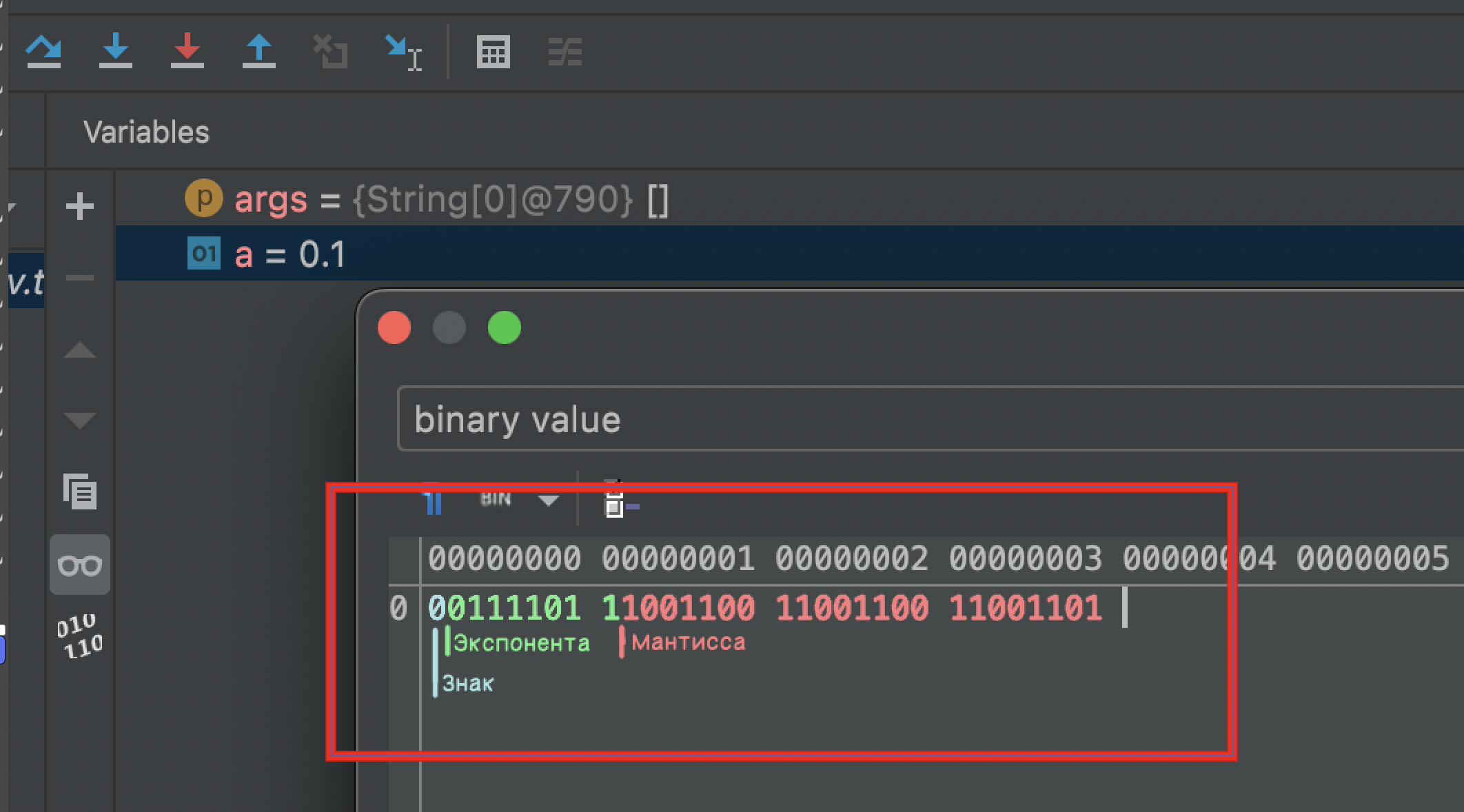
Преобразуя эту структуру обратно в десятичную систему, получим 0.10000000149012, хотя IDEA дополнительно округляет это значение до 0.1.
Проведем еще один небольшой эксперимент: найдем минимальное число, которое не будет округляться до 0.1.

Выводы
программирование — это не всегда математика
Из этой статьи вы узнали, как вещественные числа хранятся в памяти компьютера, и почему это создает проблемы.
Возможно, у вас возник вопрос: "Как мы запускаем ракеты в космос с такими неточными расчетами? Или как проходят финансовые операции?" Для выполнения вычислений без потери точности используются специальные классы, такие как BigDecimal. Этот класс позволяет складывать числа произвольной длины без потери точности, но за это приходится платить уменьшением производительности.
В заключении хочется сказать: таков удивительный мир программирования.

